脳log[ProjectEuler: 2019-01-15～]

最終更新: 2019-01-15T14:13+0900

♪ [ProjectEuler] Problem 29

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

普通に手続き的に書けば一瞬で答えが出る問題だったのに、前回も今回も(同じ)プログラムのバグのために答えが出なくて、でも素因数分解して漏れなく重複なく数えることもできなくて困っていた。バグが取れたので答えを出すのはコンピュータに任せる。

#!rubyw
# coding: utf-8

h = {}
(2..100).each{|b|
	(2..100).inject(b){|_,|
		_ *= b
		h[_] = _
	}
}
p h.size

最終更新: 2019-01-16T18:40+0900

♪ [ProjectEuler] Problem 32

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

(そういえば以前も何度となく同じことを書いていたなと思い出しながら)泥臭く手を動かしただけ。

#!rubyw
# coding: utf-8

Digits = *1..9
found = {}
(1..2).each{|_|
	Digits.combination(_){|l_cmb|
		l_cmb.permutation{|l| l = l.join('').to_i
			Digits.combination(5-_){|r_cmb|
				r_cmb.permutation{|r| r = r.join('').to_i
					p = l * r
					found[p] = "#{l} * #{r} = #{p}" if /^(?:([1-9])(?!.*\1)){9}$/ =~ "#{l}#{r}#{p}"
				}
			}
		}
	}
}
p found.keys.inject(&:+)

最終更新: 2019-01-15T16:36+0900

♪ [ProjectEuler] Problem 33

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

ただ手を動かしただけ。

#!rubyw
# coding: utf-8
require 'mathn'

found = []
(1..9).each{|numer|
(1..9).each{|denom|
	frac = numer / denom
	(numer+1..9).each{|cancel／|
		found.push("#{numer}#{cancel／}/#{cancel／}#{denom}") if frac == (numer*10 + cancel／) / (cancel／*10 + denom)
	(1..denom-1).each{|cancel＼|
		found.push("#{cancel＼}#{numer}/#{denom}#{cancel＼}") if frac == (cancel＼*10 + numer) / (denom*10 + cancel＼)
	}}
}}
p found
p found.map(&:to_r).inject(&:*).denominator

最終更新: 2019-01-15T17:32+0900

♪ [ProjectEuler] Problem 35

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

以前は require 'prime' を避けてた気がするけど、今回は使ってる。そうすると、ただコードに落とすだけ。

#!rubyw
# coding: utf-8
require 'prime'
require 'set'

primes = Prime.each(1_000_000).to_set
primes = primes.select{|p|
	s = "#{p}#{p}"
	l = s.length/2
	(1..l-1).all?{|i|
		primes.include? s[i, l].to_i(10)
	}
}
p primes
p primes.size

最終更新: 2019-01-15T21:09+0900

♪ [ProjectEuler] Problem 36

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

例によって手を動かしただけ。

#!rubyw
# coding: utf-8

PalindromeGen = lambda{|digits|
	return Enumerator.new{|y|
		_next = lambda{|a|
			return digits.map{|_|
				a.map{|p10|
					"#{_}#{p10}#{_}"
				}
			}.flatten
		}
		odd  = *digits
		even = digits.zip(digits).map{|_| _.join('') }
		yielder = lambda{|p| y << p}
		loop {
			odd = _next[odd.each(&yielder)]
			even = _next[even.each(&yielder)]
		}
	}
}
p10gen = PalindromeNGen["0".."9"]
p2gen  = PalindromeNGen["0".."1"]
found = {}
loop {
	p10 = p10gen.next.to_i(10)
	break if 1_000_000 < p10
	p2gen.next    while p2gen.peek.to_i(2) <  p10
	found[p10] = p10 if p2gen.peek.to_i(2) == p10
}
p found.keys.map{|_| [_.to_s(10), _.to_s(2)] }
p found.keys.inject(&:+)

最終更新: 2019-01-15T23:54+0900

♪ [ProjectEuler] Problem 37

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

手を動かしただけ。

#!rubyw
# coding: utf-8
require 'prime'
require 'set'

primes = Set.new
found = {}
Prime.each{|p| p = p.to_s(10)
	primes << p
	next if p.length == 1
	next unless (1..(p.length-1)).all?{|w| primes.include? p[0,w] }
	next unless (1..(p.length-1)).all?{|i| primes.include? p[i,p.length-i] }
	p found[p] = p
	break if found.size == 11
}
p found.keys.map(&:to_i).inject(&:+)

最終更新: 2019-01-16T18:01+0900

♪ [ProjectEuler] Problem 38

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

手を動かしただけ。

#!rubyw
# coding: utf-8

found = {}
i = 1
9.downto(2){|n|
	loop {
		s = (1..n).map{|_| _*i }.join('')
		break if 9 < s.length
		i += 1
		next if s.length < 9
		next if s.index "0"
		found[s.to_i] = [i-1, 1..n] unless /(.).*\1/ =~ s
	}
}
p found
p found.keys.sort.reverse

最終更新: 2019-01-16T00:54+0900

♪ [ProjectEuler] Problem 41

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。

素数って実はありふれてるので９桁までの素数を列挙するだけで許容時間(１分間)をオーバーしてしまう。９桁の順列(362880通り)を列挙して素数判定する方が早い。

#!rubyw
# coding: utf-8
require 'prime'

found = ("1".."9").map{|n|
	("1"..n).to_a.permutation.map{|_| _.join('').to_i }.select(&:prime?)
}.flatten
p found.sort.reverse

最終更新: 2019-01-16T03:47+0900

♪ [ProjectEuler] Problem 54

面倒くさくて飛ばした問題にチャレンジ。

poker.txt の内容は本当にランダムなのか３番目までの高い役が１個も入ってなくて、コーディングの苦労が報われない。

#!rubyw
# coding: utf-8

Order = "23456789TJQKA"
flush = lambda{|cards|
#	p ["flush", cards] if (cards.match(/^ .(.)(?: .\1){4}/)||[])[1]
	(cards.match(/^ .(.)(?: .\1){4}/)||[])[1]
}
straight = lambda{|cards|
#	p ["straignt", cards] if cards.scan(/ (.)/).map{|_,| Order.index _ }.sort.tap{|_| break _ == (_[0].._[0]+4).to_a ? Order[0] : nil }
	cards.scan(/ (.)/).map{|_,| Order.index _ }.sort.tap{|_| break _ == (_[0].._[0]+4).to_a ? Order[0] : nil }
}
four = lambda{|cards|
	p ["four", cards] if cards.scan(/ (.)/).sort.join('').scan(/(.)\1{3}/).map{|_,| _ }[0]
	cards.scan(/ (.)/).sort.join('').scan(/(.)\1{3}/).map{|_,| _ }[0]
}
three = lambda{|cards|
#	p ["three", cards] if cards.scan(/ (.)/).sort.join('').scan(/(.)\1{2}/).map{|_,| _ }[0]
	cards.scan(/ (.)/).sort.join('').scan(/(.)\1{2}/).map{|_,| _ }[0]
}
pairs = lambda{|cards|
#	p ["pairs", cards] unless cards.scan(/ (.)/).sort_by{|_,| - Order.index(_) }.join('').scan(/(.)\1/).map{|_,| _ }.empty?
	cards.scan(/ (.)/).sort_by{|_,| - Order.index(_) }.join('').scan(/(.)\1/).map{|_,| _ }
}
highcards = lambda{|cards|
#	p ["highcards", cards]
	cards.scan(/ (.)/).sort.join('').gsub(/(.)\1+/, '').split(//).sort_by{|_| - Order.index(_) }
}
fullhouse = lambda{|cards|
#	p ["fullhouse", cards] if pairs[cards].length == 2 and three[cards]
	pairs[cards].length == 2 and three[cards]
}
straightflush = lambda{|cards|
	suit = flush[cards]
	first = straight[cards]
	p ["straightflush", cards] if suit and first
	suit and first
}
royalflush = lambda{|cards|
	first = straightflush[cards]
	p ["royalflush", cards] if first and first == 'T'
	first and first == 'T'
}

compare = lambda{|h|
	h.map{|_| Array(_).map{|_| _ ? Order.index(_)||-1 : -2 } }.tap{|h| break h.first.length != h.last.length ? h.first.length <=> h.last.length : h.first <=> h.last }
}

contest = lambda{|c|
	[royalflush, straightflush, four, fullhouse,
	 flush, straight, three, pairs, highcards
	].each{|ranktest|
		h = c.map(&ranktest)
		return compare[h] if h.any?{|_| _ and not _.empty? }
	}
	raise "no contest"
}

p DATA.lines.map{|ln|
	p1 = " " + ln[0, 15]
	p2 = ln[14, 15] + " "
	contest[[p1, p2]]
}.count(1)

__END__
content of poker.txt here.

最終更新: 2019-01-14T23:35+0900

♪ [ProjectEuler] Problem 27

解けなくて飛ばした問題の中で一番最初の問題に再チャレンジ。a の定義、b の定義、b が限界を定める、というところから、あとは計算。15 秒くらいかかってもいいでしょう。

#!rubyw
# coding: utf-8
require 'prime'

a = *-1000..0
b = Prime.each(1000).reject {|_| _ < 80 }
remains = a.product b
(0..1000).each {|n|
	remains.reject! {|a, b|
		n     ==  b or
		n + a == -b or
		(n * (n + a) + b) <= 0 or
		not (n * (n + a) + b).prime?
	}
	puts "remains #{remains.size}"
	puts "a = %d; b = %d; n = %d" % [*remains[0], n] if remains.size == 1
	break if remains.size <= 1
}

最終更新: 2021-09-14T21:45+0900

♪ [ProjectEuler] Problem 191

 Problem 191

別個に知っているが関連があるとは思っていなかった二つの Webサイト、「ときどきの雑記帖 再起編 2012年2月(中旬)」から「Problem 191 - もうカツ丼でいいよな」へのリンクがどういう観点で張られたのか、確かめるために*リンク先を読みたいがネタバレはいかん。との思いでがんばった。

まず問題がおかしい。欠席は３連続でなければ許されるのに遅刻は１回までとか⁑。まあどうでもいい。それより問題文が難しかった。punctuality(無遅刻)と forfeit(権利の喪失)の２単語は辞書を引いたし、カンマや関係詞で連続する文は主語述語修飾関係がわかりにくいので、細かいことを考えずに流れに注意して４、５回読み直した。81という数字がどういう経緯で出てきたのか(※OALの３文字で作る長さ４の文字列=3^4通り)、説明があれば問題文を理解する一助となったろうに、そんなものはなかった。

Half_period_strings行以降のバグてんこ盛りのぐだぐだは一重に処理時間と消費メモリを節約することが目的。正規表現でやることは最初からの方針だったのだけど改行で連結した 30-period stringsを検索しようとしたら Rubyがメモリ不足で落ちる。ワーキングセットが 2GiBを超えたあたりだったと思う。ならばと一行分ずつ逐一処理しようとすると時間がかかりすぎる(30分はかからないが)。Threadで分散してみようとしたが Ruby(1.9)には GVLとかいうのがあって CPUを 33%までしか使ってくれなかった。Fiberもそういう期待には応えてくれないみたい。プロセス間通信は面倒。時間が許すなら、

Thirty_period_strings = Joint_period_strings[
	Fifteen_period_strings, Fifteen_period_strings
]
p Thirty_period_strings.inject(0){|count,tristr|
	count + 1 + tristr.scan(/A|(?<=AA)O|(?<=A)O(?=A)|O(?=AA)/).length
}

これ(を配列を要求しないように書き換えたバージョン)だけで済んでしまうことなのに、15-period stringsと 30-period stringsの間には処理すべき量に雲泥の差があった。

戦略は、

• 一つまでしか許容されない Lをひとまず無視(scoreというのが Lの持ち込む派生語の数に関連した値)。
• (現実的に扱える量である)15-period stringsの連結を考える。

以下、偶然なのかなんなのか、答えは出たが説明できないスクリプト(ピリオドの置き方が Ruby 1.9専用みたい)。実行時間は１秒未満。

# PE 191

Letters = %w(O A).freeze
Re_filter = /^(?:(?!AAA).)*$/
Joint_period_strings = lambda{|*args|
	return args.first.product(*args.drop(1))
		.map{|_| _.join('') }
		.select{|_| _.match(Re_filter) }
}
Three_period_strings = Joint_period_strings[
	Letters, *Array.new(2){ Letters }
].freeze
Six_period_strings = Joint_period_strings[
	Three_period_strings, Three_period_strings
].freeze
Fifteen_period_strings = Joint_period_strings[
	Six_period_strings, Six_period_strings, Three_period_strings
].freeze
Re_score = /A|(?<=AA)O|(?<=A)O(?=A)|O(?=AA)/
IndexedScore = Struct.new(:num, :sum)

Half_period_strings = Fifteen_period_strings

l_index = Hash.new{|h,l_back| h[l_back] = IndexedScore.new(0,0) } # by ending codon. {'OOO'=>IndexedScore,'OOA'=>,...}
r_index = lambda{|r_front| return l_index[r_front.reverse] } # by starting codon. {同上} (実体はl_indexと共有)
Half_period_strings.each{|str15|
	score = l_index[str15[-3,3]]
	score.num, score.sum = score.num+1, score.sum+str15.scan(Re_score).length
}
p l_index.keys.product(l_index.keys).inject(0){|count,_| l_back, r_front = *_
	joint = l_back + r_front
	next count if Re_filter !~ joint
	l_score, r_score = l_index[l_back], r_index[r_front]
	joint_score = [joint, l_back, r_front].map{|_| _.scan(Re_score).length }.inject{|a,b| a-b }
	next count + l_score.sum*r_score.num + r_score.sum*l_score.num + (1+joint_score)*l_score.num*r_score.num
}
p Process.times

 @2012-02-15

他所を見て回った。得たヒントは「漸化式」「DP」「scoreは Oを数えるだけ」「prize stringは Lの出現回数(0-1)と先端部の Aの連続数(0-2)で classifyできる」。

 「scoreは Oを数えるだけ」

実際、どちらでもいけた。だけど下の方が良いのは明らか。ビットを数える処理にも置き換えられるし、joint_scoreは不要になるし。

score = tristr.scan(/A|(?<=AA)O|(?<=A)O(?=A)|O(?=AA)/).length
score = tristr.count(?O)

 「prize stringは Lの出現回数(0-1)と先端部の Aの連続数(0-2)で classifyできる」

このヒントを基に以下のスクリプトができた。実行時間はコンマ１秒未満。１０倍高速。早く書けてバグが無くて実行が速くて、昨日と一昨日の自分が何に頭を悩ませてたのか不思議になるよね。この着想に独力でたどり着けないところが己の限界。

# coding: utf-8
# PE 191

Extend_prize_strings = lambda{
	L,A,O = 1,1,1
	A0L0, A0L1, A1L0, A1L1, A2L0, A2L1 = *0..5
	return lambda{|prize_strings| ❦=prize_strings
		return [
		# a=0; l=0
			❦[A0L0]*O + ❦[A1L0]*O + ❦[A2L0]*O,
		# a=0; l=1
			❦[A0L0]*L + ❦[A0L1]*O + ❦[A1L0]*L + ❦[A1L1]*O + ❦[A2L0]*L + ❦[A2L1]*O,
		# a=1; l=0
			❦[A0L0]*A,
		# a=1; l=1
	 		❦[A0L1]*A,
		# a=2; l=0
			❦[A1L0]*A,
		# a=2; l=1
			❦[A1L1]*A
		]
		# a=3 (prize forfeited)
			❦[A2L0]*A
			❦[A2L1]*A
		# l=2 (prize forfeited)
			❦[A0L1]*L
			❦[A1L1]*L
			❦[A2L1]*L
	}
}.call

Period = 30

# index of prize_strings: i = (a<<1)|l
# a = consecutive As at a prize string head. (0,1,2)
# l = occasion of L. (0,1)
# starting state(=prize string length is zero): a=0;l=0;prize_strings[i]=1
prize_strings = [1,0,0,0,0,0]
Period.times{
	prize_strings = Extend_prize_strings.call prize_strings
}
p prize_strings.inject(&:+)
p Process.times

C++11だとコンパイル時に答えを出してしまいそうだ。再帰30回だし。

最終更新: 2012-01-20T00:09+0900

♪ [ProjectEuler] Problem 10, 12, 14, 17, 19, 21, 23

穴埋め。解ける問題がはやなくなってきたから……(完全になくなってはいないはずっ)。

 Problem 10

時間コストを空間コストに置き換えて。

arr = [true] * 2_000_000
sum = 0
2.upto(arr.size-1){|i|
	next unless arr[i]
	sum += i
	i.step(arr.size-1, i){|j|
		arr[j] = false
	}
}
p sum
p Process.times

 Problem 12

Rubyに頼った。prime_divisionのこと。

require 'mathn'

trinums = lambda{
	tri, n = 0, 1
	return lambda{
		tri, n = tri+n, n+1
		return tri
	}
}.call

loop{
	tri = trinums.call
	div = tri.prime_division.inject(1){|d,_| f,e = *_; d*(e+1) }
	if 500 < div
		puts tri
		p Process.times
		exit
	end
}

 Problem 14

ゴールから攻めようとか小賢しいことは考えずに。

number_of_chain = lambda{
	memo = {1=>1}
	this = lambda{|n|
		return memo[n] || (memo[n] = 1 + this[n%2==0 ? n/2 : 3*n+1])
	}
	return this
}.call

p (1...1_000_000).max_by{|_| number_of_chain[_] }
p Process.times

 Problem 17

面倒なだけ。

cc = lambda{
	return this = lambda{|n|
		count, num = 0, n

		digit1000 = num / 1000
		if 0 < digit1000
			count += this[digit1000] + 'thausand'.length
			num -= digit1000 * 1000
			count += 'and'.length if num != 0
		end

		digit100 = num / 100
		if 0 < digit100
			count += this[digit100] + 'hundred'.length
			num -= digit100 * 100
			count += 'and'.length if num != 0
		end

		digit10 = num / 10
		if 2 <= digit10
			count += {
				20=>'twenty'.length,
				30=>'thirty'.length,
				40=>'forty'.length,
				50=>'fifty'.length,
				60=>'sixty'.length,
				70=>'seventy'.length,
				80=>'eighty'.length,
				90=>'ninety'.length,
			}[digit10*10]
			num -= digit10 * 10
		end

		if num != 0
			count += {
				1=>'one'.length,
				2=>'two'.length,
				3=>'three'.length,
				4=>'four'.length,
				5=>'five'.length,
				6=>'six'.length,
				7=>'seven'.length,
				8=>'eight'.length,
				9=>'nine'.length,
				10=>'ten'.length,
				11=>'eleven'.length,
				12=>'twelve'.length,
				13=>'thirteen'.length,
				14=>'fourteen'.length,
				15=>'fifteen'.length,
				16=>'sixteen'.length,
				17=>'seventeen'.length,
				18=>'eighteen'.length,
				19=>'nineteen'.length
			}[num]
		end
		return count
	}
}.call

p (1..1000).inject(0){|sum,n| sum + cc[n] }

 Problem 19

問題文が難しかった。閏年の条件として "A leap year occurs on any year evenly divisible by 4, but not on a century unless it is divisible by 400." って書いてあったけど、centuryって XX01年から XY00年の 100年間を指す語だと思ってるから、"a century"が XY00年のことだけを示してるとは思わなくて、結果的に 100の条件を読み飛ばした上に 400の条件を逆にとらえてた。

days_of_month = lambda{|year,month|
	return 31 if [1,3,5,7,8,10,12].include?(month)
	return 30 if [4,6,9,11].include?(month)
	return 29 if year % 400 == 0
	return 28 if year % 100 == 0
	return 29 if year % 4 == 0
	return 28
}

dow = 1 # 日月火水木金土=0123456. 1=Monday. 1900-01-01 was a Monday.
(1..12).each{|month|
	dow = (dow + days_of_month[1900,month]) % 7
}
# Now dow indicates the day of 1901-01-01.

count = 0
(1901..2000).each{|year|
	(1..12).each{|month|
		count += 1 if dow == 0
		dow = (dow + days_of_month[year,month]) % 7
	}
}
p count

 Problem 21

愚直に(←これしか書いてなくない？)。

d = lambda{|n|
	divsum = 1
	t, tmax = 2, n
	while t < tmax
		q, r = *n.divmod(t)
		divsum += (t!=q ? t+q : t) if r == 0
		t, tmax = t+1, q
	end
	return divsum
}

p (1..10000).inject(0){|sum,n|
	dn = d[n]
	sum + (n < dn && d[dn] == n ? n+dn : 0)
}

 Problem 23

そのまま(←愚直にを言い換えただけ)。

class Integer
	def abundant?
		divsum = 1
		t, tmax = 2, self
		while t < tmax
			q, r = *self.divmod(t)
			divsum += (t!=q ? t+q : t) if r == 0
			t, tmax = t+1, q
		end
		return self < divsum
	end
end

expressible = [false] * (28123+1)
abundant = []
(1..(28123-12)).select(&:abundant?).each{|n|
	abundant << n
	abundant.each{|a|
		break if expressible.size <= a+n
		expressible[a+n] = true
	}
}
p (1..28123).inject(0){|sum,n| sum + (expressible[n] ? 0 : n) }

最終更新: 2011-10-29T21:40+0900

♪ [ProjectEuler] Problem 333

 Problem 333

何時間もかかるこれがどうやったら速くなるでしょうか？

いまは可能な組み合わせを全て試してみて、できあがった数字をカウントしてる。その後で素数を順番に辿って生成カウントが 1のものを足し合わせたものが答え。上限が 10倍になるごとにどえらく計算量が増える。かけ算ならまだしも足し算の組み合わせに有効な考え方を自分が全く持ち合わせていないことがこれまでの問題からも何となくわかってる。どうすんの？

# PE333
require 'mathn' # Primeが使いたいだけなのに。グローバルフラグは悪。
UPPERBOUND = 100_0000
EXP3_UPPERBOUND = (Math.log(UPPERBOUND)/Math.log(3)).floor+1
EXP2_UPPERBOUND = (Math.log(UPPERBOUND)/Math.log(2)).floor+1

#  ×  2^0 2^1 2^2 2^3 2^4 2^5 2^19
# 3^0  1   2   4   8  16  32  524288
# 3^1  3   6  12  24  48  96
# 3^2  9  18  36  72
# 3^3 27  54
# 3^4 81
# 3^5
# 3^12 531441

primes = Hash.new(0)
q = []
sum_of_q = lambda{
	sum = 0
	last_exp3 = EXP3_UPPERBOUND
	q.each_with_index{|exp3,exp2|
		next if exp3 == last_exp3
		sum += (1<<exp2) * 3**exp3
		last_exp3 = exp3
	}
	return sum
}
fill_q = lambda{
	q.fill(q.last||EXP3_UPPERBOUND, q.length, EXP2_UPPERBOUND-q.length);
}
fill_q.call
until q.empty?
	exp2, pow2 = q.length-1, 1<<(q.length-1)

	next q.pop if q[exp2] == 0
	q[exp2], pow3 = q[exp2]-1, 3**(q[exp2]-1)
	sum = sum_of_q.call
	q[exp2], pow3, sum = q[exp2]-1, pow3/3, sum-(2*pow2*pow3/3) while 0 <= q[exp2] and UPPERBOUND <= sum
	next q.pop if q[exp2] < 0

	primes[sum_of_q.call] += 1
	fill_q.call
end

sum = 0
Prime.new.each{|pr|
	break if UPPERBOUND <= pr
	sum += pr if primes[pr] == 1
}
p sum
p Process.times #=> <struct Struct::Tms utime=25990.64, stime=150.806, cutime=0.0, cstime=0.0>

最終更新: 2013-05-18T14:03+0900

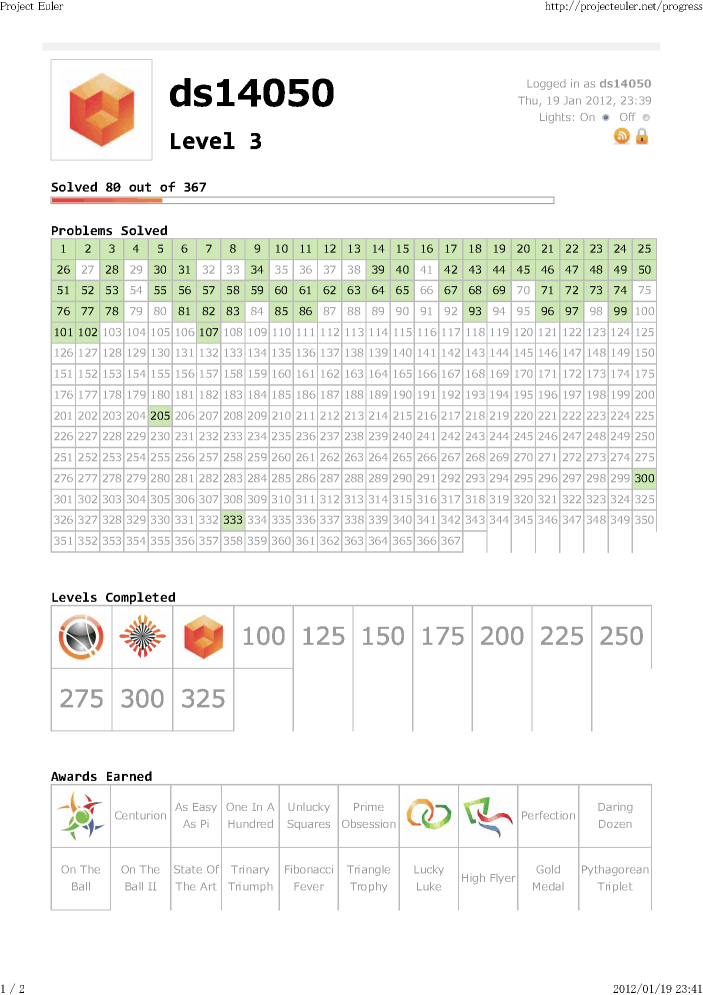
♪ [ProjectEuler] Problem 205, Problem 300

 Problem 205

行き詰まっている。新しくなった Progress画面でテキトーに問題をクリックしたら勝率の高い(正答者数の多い)問題だったでござる。

# さいころふりふり
total4 = [0,1,1,1,1] + [0]*32 # サイコロを 1回振って出目(o)の合計が i(=1,2,3,4,...,36)である場合の数を total4[i]。0番目は単なるプレースホルダ。
8.times{ # 2-9回目
	(total4.size-1).downto(1){|i|
		total4[i] = (1..([4,i].min)).inject(0){|sum,o| sum + total4[i-o] }
	}
}
total6 = [0,1,1,1,1,1,1] + [0]*30
5.times{
	(total6.size-1).downto(1){|i|
		total6[i] = (1..([6,i].min)).inject(0){|sum,o| sum + total6[i-o] }
	}
}
# 集計
win4 = 0
sum4, sum6 = 0, 0
1.upto(36){|total|
	win4 += total4[total] * sum6
	sum4, sum6 = sum4 + total4[total], sum6 + total6[total]
}
p 1.0*win4/sum6/sum4

 Problem 300

5時間以上かかった……(実行に)。

Process.times: #<struct Struct::Tms utime=20471.855, stime=8.268, cutime=0.0, cstime=0.0>

どうすれば……。

1. すべての折りたたみパターンを列挙。(点対称は除いたつもり。鏡像はそのまま。593611通り)
2. パターンをコンタクトポイント(インデックスのペア)列に変換|sort|uniq。(12495通り)
3. すべてのタンパク(2^{15}通り)をさっき求めたコンタクトポイントの列(12495通り)に当てはめて(約408701758通り)、最良の H-Hコンタクトポイント数の合計を得る。

何の工夫もないナイーブなやり方だから手を付ける余地はあり余ってるんだろうけど、どういうやり方をしたらいいのか途方に暮れる。

スレッドを見たら先頭から 3つ 4つ立て続けに「brute force」の文字。それでも 20秒やら 3分で終わるらしい。バブルソートと同じくバカの代名詞(※ごく少数を対象にするなら妥当な選択肢)みたいに思ってるけど、その中でもさらに利口なのとバカなのとがあるのね。最低限のたしなみとして作業領域の大量コピーはしてないんだけど。

最初は 6時間かかったけど 12分に縮まったという人もいた。そういうことならもう少し手を入れてみよう。

 @2011-09-27

 1.折りたたみパターンの列挙

• 団子(直線や突起を含む)か、1つ以上の連結したドーナツ状になるしかない。
• 団子がコンタクトポイント数を稼ぐのに一番有利。

というあたりでひとつ(どうにかならないか？)。

おっと、ドーナツになるとコンタクトポイントにボーナス(+1)が付くのだった。

 2. 12495通りのコンタクトポイント列

• 頭としっぽの区別をなくしたら、半分とはいかないまでも減る。不可
• 他ののサブセットになってるのがあったら除外できる。12495→3409通り

 3. すべてのタンパク(2^{15}通り)をコンタクトポイントの列(12495通り)に当てはめる。(408701758通り)

手立てなし。

ステップ2でサブセットを除去したら 2分。ただし C++で。

最適化オプションを目に付いただけくっつけただけで 15秒になるんだもんな。>PE300.cpp C++で 3秒だという人がいるけど、これ以上の悪足掻きをするかは微妙。

しかしまあ、投稿されたコードを眺めると、アホな人間は自分から問題を難しくしてそれに四苦八苦してるような印象を受ける。自虐してるの？ 要するに、上にアップロードしたコードはもっとシンプルに書けるはずだ、と。HとPの長さ15の配列としてのタンパクを 0から 2^{15}未満の整数のビットパターンで表したり……。手立てなしとしたステップ3こそが実行時間の大半を占めてるので高速化のメインステージなのだ。再帰してる場合でも vectorをループで回してる場合でもないのだ。こういう筋トレっぽいトレーニングをしてくれる問題は貴重。これまで考えたことがないから。

 2011-10-17

優れた人々は無意識にやっているので、あまりこういうことは教えてもらえない(というか当然やっていますよねJK、などと思われていたりする)ので本書のように、あらためて書いてくれている本は大変貴重だと思った次第。すごい人達が「ナイーブな手法でいいんじゃね」という時は「本書で書いてあるようなことを当然踏まえた上で適切にナイーブな手法を組み合わせて使っている」という意味だったりするので十分注意したい。

ナイーブという単語に反応した。上の方で「何の工夫もないナイーブなやり方だから手を付ける余地はあり余ってるんだろうけど」と書いたときのナイーブはもちろん……。練習問題、やります。

 @2012-03-03

C++で３秒だという人のコードを読んでいた。自分でコードできるほど十分には理解してないけど見つけたアイディアだけ書いてみる。

for (auto a = s.begin(); a != s.end(); ++a) {
    bitset<64> _t = t & *a;
    m = max(m, (int)_t.count());
}

タンパク質(t)とコンタクトポイント列(a)が long long intで、sはコンタクトポイント列の集合。コンタクトポイント列とタンパク質の照合が bitwise andで済んでしまっている。

俺が vector<pair<char,char> >としたコンタクトポイント列がどのように long long intにパッキングされているのか。

 ペアの大小。

pair<char,char>は、タンパク質の先頭からのインデックス(0..14)を使って、(4,9)も (9,4)も表現できるが両者は同じなので (9,4)だけ表せればいい。インデックス iの(i+1番目の)アミノ酸とペアになりうるインデックスは全部で i種類。これなら必要ビット数は \sum_{i=0}^{14}i = 105。

 ペアの偶奇。

チェス盤の黒白を考えるとわかりやすいけど、黒いマスの隣には白いマスしかない。インデックスが奇数のアミノ酸(H,P)の隣にはインデックスが偶数のアミノ酸しかこない。これで情報を失わずに表現形を半分に減らせる。\sum_{i=0}^{14}\lceil\frac{i}{2}\rceil = \sum_{i=0}^{14}\lfloor\frac{i+1}{2}\rfloor = 56ビット(→床関数)。long long intに収まるサイズになった。

と、ここまで読んだ*んだけど、15ビット以上の整数型で表されるタンパク質を照合用の56ビット表現に変換するところの解読がまだ。プログラム全体としては無駄がなくて、そういう意味ではわかりやすいんだけど。(L=15; int hを long long int tに変換)

long long int t = 0;
for (int i = 0; i < L; ++i) {
    t <<= ((i + 1) / 2);
    if (h & (1 << i))
        for (int j = (i + 1) % 2; j < i; j += 2)
            if (h & (1 << j))
                t |= 1 << (j / 2);
}

最終更新: 2011-09-17T21:10+0900

♪ [ProjectEuler] Problem 102, Problem 107

 Problem 102

説明はできない。条件は二つで足りると思ったが間違いだったので三つにした。そうしたら通った。

require 'matrix'
AX, AY, BX, BY, CX, CY = 0,1,2,3,4,5
O = Vector[0,0]
count = 0
DATA.each_line{|ln|
	nums =  ln.chomp.split(',').map(&:to_i)
	a, b, c = Vector[nums[AX],nums[AY]], Vector[nums[BX],nums[BY]], Vector[nums[CX],nums[CY]]
	ab, ao, ac = b-a, O-a, c-a
	bc, bo, ba = c-b, O-b, a-b
	ca, co, cb = a-c, O-c, b-c
	ab_cosOAB, ab_cosCAB = ao.inner_product(ab) / ao.r, ac.inner_product(ab) / ac.r
	bc_cosOBC, bc_cosABC = bo.inner_product(bc) / bo.r, ba.inner_product(bc) / ba.r
	ca_cosOCA, ca_cosBCA = co.inner_product(ca) / co.r, cb.inner_product(ca) / cb.r
	count += 1 if ab_cosOAB >= ab_cosCAB and bc_cosOBC >= bc_cosABC and ca_cosOCA >= ca_cosBCA
}
p count
__END__
content of triangles.txt here.

一応の説明を試みると、三本の辺それぞれから見て、辺を構成しない頂点が原点より見上げる位置にあるどうかをコサインの大小で判定してる。ただ、コサインは X軸対称なので見上げてるのか見下ろしてるのかは実際のところわからない。だから二つの辺では不十分で、三つの辺すべてで判定しなければいけない。※この最後の文ではやっぱり説明できてない気がする。

検索した。外積なんて(言葉しか)知りません。問題文の「Cartesian plane」もわからなかったので無視したんだった。なんで Cartesianがデカルトになるの？

 Problem 107

メソッド名を決めるまでで 9割が終わってる。

軽い辺から順番に有効にしていき、有効な辺のみで最初にすべての頂点を通ることができたとき、最後に有効にした辺、この辺は隣接する点のうち最も離れている二つを結ぶ最短経路。これより軽い辺を組み合わせてこの二点を結ぶことはできないし、これより重い辺を組み合わせて結ぶのは不必要な無駄を抱える。あとは、このように確定した辺の両端を一個の点とみなすようにしながら再帰的に確定していく。

def find_the_required_edge_with_maximum_weight(matrix)
	active_edge = Hash.new{|h,k| h[k] = {} }
	(0...matrix.size).map{|src|
		((src+1)...matrix.size).reject{|dst| matrix[src][dst].nil? }.map{|dst|
			[src,dst]
		}
	}.inject(&:+).sort_by{|src, dst| matrix[src][dst] }.each{|src, dst| # lighter edge first
		active_edge[src][dst] = active_edge[dst][src] = true

		visited = [false] * matrix.size
		firstvisit = {src=>true, dst=>true}
		until firstvisit.empty?
			v = firstvisit.shift[0]
			visited[v] = true
			if visited.all?
				return [src, dst]
			end
			active_edge[v].each{|nxt,|
				firstvisit[nxt] = true unless visited[nxt]
			}
		end
	}
	return nil
end

matrix = DATA.lines.map{|ln| ln.chomp.split(",").map{|_| _ == '-' ? nil : _.to_i } }
sum_of_weight = matrix.map{|row| row.compact.inject(&:+) }.inject(&:+) / 2
reduced_sum_of_weight = 0
loop{
	src, dst = *find_the_required_edge_with_maximum_weight(matrix)
	weight = matrix[src][dst]
	break if weight == 0
	reduced_sum_of_weight += weight

	matrix[src][dst] = matrix[dst][src] = 0
	matrix.map!{|row| row.map!{|_| _ && weight < _ ? nil : _ } }
}
puts "#{sum_of_weight - reduced_sum_of_weight} saved. (#{sum_of_weight} -> #{reduced_sum_of_weight})"

__END__
content of network.txt here.

もう限界が近いのですよ。風呂の中でああでもないこうでもないと考えてやっと辿り着いたのが上の答え。sum_of_weightの割る 2は忘れるので注意。

Problem 107を検索した。→「最小全域木」「プリム法」「クラスカル法」

クラスカル法のつもりで書いたのが下。上のより 10倍速い。0.5秒が 0.05秒になるレベル。

matrix = DATA.lines.map{|ln| ln.chomp.split(",").map(&:to_i) }
sum_of_weight = matrix.map{|row| row.inject(&:+) }.inject(&:+) / 2
reduced_sum_of_weight = 0

trees = (0...matrix.size).map{|v| {v=>true} }
(0...matrix.size).map{|src|
	((src+1)...matrix.size).reject{|dst| matrix[src][dst] == 0 }.map{|dst|
		[src,dst]
	}
}.inject(&:+).sort_by{|src, dst| matrix[src][dst] }.each{|src, dst| # lighter edge first
	i_src, i_dst = trees.index{|tree| tree[src] }, trees.index{|tree| tree[dst] }
	if i_src != i_dst
		reduced_sum_of_weight += matrix[src][dst]
		trees[[i_src, i_dst].min].update(trees[[i_src, i_dst].max])
		trees.delete_at([i_src, i_dst].max)
		break if trees.size == 1
	end
}

puts "#{sum_of_weight - reduced_sum_of_weight} saved. (#{sum_of_weight} -> #{reduced_sum_of_weight})"

__END__
content of network.txt here.

ある段階で最短に見えた経路も木が育って起点が増えるにつれて最短でなくなることがある気がしたので、まわりくどい条件を課してたんだけど、いらん心配だったみたい。起点とか関係なしに軽い辺から繋いでるんだから、連結して起点が増えたところで、後から付け替える余地はなかった。

『[単行本] R. ブランデンベルク, P. グリッツマン【最短経路の本】 シュプリンガー・ジャパン株式会社』をもう一回読んでみよう。当時はグラフっていえば棒グラフ？ってな知識しかなかったからね。世界の秘密をひとつ覗いた気になったもんだ。ちなみに最近は非線形科学(類語：複雑系、自己組織化、創発、冪乗則)とかシステム生物学がブーム。

最終更新: 2011-09-10T23:55+0900

♪ [ProjectEuler] Problem 101

 Problem 101

(↑↑のリンク先を見て)行列を使うことがわかればなんとか。最初に考えた階差数列とか二項係数を使った手順とはなんだったのか。要の逆行列の計算(もう忘れた)は Rubyがやってくれるし。だけど最初は行列の要素が整数だったせいで正しい逆行列が得られなくてハマった。

浮動小数点数や有理数その他に対応するために、Matrix#inverseは演算の手続きだけを提供してる、ということなんだと思うけど、全くでたらめな結果が正常に返ってくるのは驚き。元の行列と逆行列の要素がどちらも整数になることがわかってる場合はなおさら。型指定がないことで扱いが難しくなってしまってる。

このへん(ja.wikipedia.org)まで理解したいなあ。

require 'matrix'

# (a0,a1,a2,a3,...) -> (n) -> a0 + a1*n + a2*n^2 + a3*n^3 +...
Poly = lambda{|*kk|
	kk.reverse!
	return lambda{|n|
		return kk.inject(0){|sum,k|
			sum * n + k
		}
	}
}
Q = [1,-1,1,-1,1,-1,1,-1,1,-1,1]
QSeq = Poly[*Q] # (n) -> 1 − n + n^2 − n^3 + n^4 − n^5 + n^6 − n^7 + n^8 − n^9 + n^10

Main = lambda{
	sum_of_FIT = 0
	a, n = [QSeq[0]], 0
	until a == Q
		aseq = Poly[*a]
		raise if aseq[n] != QSeq[n]
		n += 1 while aseq[n] == QSeq[n]
		sum_of_FIT += aseq[n]
		a = Next_OP[QSeq, n]
	end
	p sum_of_FIT
}

Next_OP = lambda{|seq, k|
	return (Matrix[
		*(1..k).map{|i| _ = [1.0]; (k-1).times{ _.push(_.last*i) }; _ }
	].inverse * Matrix[
		*(1..k).map{|_| [seq[_]] }
	]).column(0).to_a.map(&:round)
}

Main.call

最終更新: 2011-08-20T02:11+0900

♪ [ProjectEuler] Problem 96, Problem 97, Problem 99, Problem 93

 Problem 96

ナンバープレイス。30秒くらいかかります。数独ソルバは前にも書いたことがある(20100511)。その時とくらべてしたことといえば優先度を付けたくらい。場合によってそれが効果的なのは Problem 83のとき(20110325p01.03)に実感してる。

def main
	tl3digits = []
	numarr = ''
	DATA.each_line{|line| line.chomp!
		if /^\d{9}$/ =~ line
			numarr << line
			tl3digits << solve(numarr)[0,3].to_i if numarr.size == 9*9
		else
			numarr = ''
		end
	}
	puts "#{tl3digits.size} puzzles were solved."
	puts "The sum of 3-digit numbers is #{tl3digits.inject(&:+)}."
end

def solve(nums)
	pns = possible_numbers(nums) # [[index,X,Y,...],...]
	pns_shortest = 10
	pns_shortest_index = -1
	pns.each_with_index{|pn,i|
		if pn.size-1 < pns_shortest
			pns_shortest = pn.size-1
			pns_shortest_index = i
		end
	}
	if 10 <= pns_shortest
		return nums # solved!
	elsif 0 == pns_shortest
		return nil # false branch. no solution.
	else
		pn = pns[pns_shortest_index]
		index = pn.shift
		return pn.map{|n|
			nums_ = nums.dup
			nums_[index] = n
			solve(nums_)
		}.compact[0] # nil or solution
	end
end

def possible_numbers(nums)
	pns = []
	(0...9).each{|y|
		(0...9).each{|x|
			i = index(x,y)
			next unless nums[i] == ?0
			pns << [i] + ((?1..?9).to_a - determined_numbers(nums, h_indices(x,y)) - determined_numbers(nums, v_indices(x,y)) - determined_numbers(nums, b_indices(x,y)))
		}
	}
	return pns
end

def index(x,y)
	return x + y*9
end
def h_indices(x,y)
	return y*9 ... (y+1)*9
end
def v_indices(x,y)
	return (0...9).map{|y| x + y*9 }
end
def b_indices(x,y)
	i = index(x-x%3, y-y%3)
	return [i, i+1, i+2, i+9, i+10, i+11, i+18, i+19, i+20]
end
def determined_numbers(nums, indices)
	return indices.map{|i| nums[i] }.reject{|n| n == ?0 }
end

main;

__END__
content of sudoku.txt here.

 Problem 97

Bignumがある Rubyでは関係ないけど、64ビット整数を前提に小細工(ループ展開)。

ten = 56866
978807.times{
	ten = (ten * 256) % 10000000000
}
p (ten + 1) % 10000000000

 Problem 99

場違いに簡単な問題。

max_lineno, max_number = 0, 0
lineno = 0
DATA.each_line{|line| line.chomp!; next if line.empty?; lineno += 1
	base, exp = *line.split(",", 2).map(&:to_i)
	number = exp * Math.log(base)
	max_lineno, max_number = lineno, number if max_number < number
}
p max_lineno
__END__
content of base_exp.txt here.

 Problem 93

スクリプトは不完全。4つの数{1,2,5,8}と四則演算とカッコを使って 36を作る方法がわからない。

Ops = [:+, :-, :*, :/].freeze
Ops3 = Ops.product(Ops, Ops).freeze
max_fnxn = 0 # fnxn: first non-expressive number
max_fnxn_c4 = nil
(0..9).to_a.combination(4){|c4|
	xns = [true]
	c4.permutation.to_a.product(Ops3).each{|_| nums, ops = *_
		num = nums.last.to_f
		3.times{|i|
			num = num.send(ops[i], nums[i])
		}
		xns[num.to_i] = true if num.finite? and 0 < num.to_i and num.ceil == num.floor
	} # 24 * 64
	fnxn = xns.index(nil) || xns.length
	if max_fnxn < fnxn
		max_fnxn = fnxn
		max_fnxn_c4 = c4
	end
} # 210
puts "{#{max_fnxn_c4.sort.join(',')}} forms 1 to #{max_fnxn-1} numbers."

例えば、(5 - (1/2)) * 8 = 36。数字の順列 ABCDと演算子の順列___をそのまま連結して A_(B_(C_D)) を作るだけでは全ての式を網羅できてなかった。左右対称になるのを除いて、次の 3通りに順列と順列を組み合わせた。((A_B)_C)_D, (A_(B_C))_D, (A_B)_(C_D)

Ops = [:+, :-, :*, :/].freeze
Ops3 = Ops.product(Ops, Ops).freeze
Evaluate = lambda{|exp|
	s = []
	until exp.empty?
		h = exp.shift
		if h.kind_of?(Symbol)
			s[-2] = s[-2].send(h, s[-1])
			s.pop
		else
			s.push(h)
		end
	end
	return s[-1]
}
max_fnxn = 0 # fnxn: first non-expressive number
max_fnxn_c4 = nil
(0..9).to_a.combination(4){|c4|
	xns = [true]
	c4.map(&:to_f).permutation.to_a.product(Ops3).each{|_| nums, ops = *_
		[
			[nums[0], nums[1], ops[0], nums[2], ops[1], nums[3], ops[2]], # ((A_B)_C)_D
			[nums[0], nums[1], nums[2], ops[0], ops[1], nums[3], ops[2]], # (A_(B_C))_D
			[nums[0], nums[1], ops[0], nums[2], nums[3], ops[1], ops[2]]  # (A_B)_(C_D)
		].each{|exp|
			num = Evaluate.call(exp)
			xns[num.to_i] = true if num.finite? and 0 < num.to_i and num.ceil == num.floor
		} # 3
	} # 24 * 64
	fnxn = xns.index(nil) || xns.length
	if max_fnxn < fnxn
		max_fnxn = fnxn
		max_fnxn_c4 = c4
	end
} # 210
puts "{#{max_fnxn_c4.sort.join(',')}} forms 1 to #{max_fnxn-1} numbers."

最終更新: 2011-08-20T02:12+0900

♪ [ProjectEuler] Problem 85

 Problem 85

incorrect

Target = 2_000_000
Size = Math.sqrt(Target*2).floor+1
a = (1..Size).map{|i| i*(i+1)/2 }
answer = 0
until a.empty?
	jv = a.last
	answer = [a.map{|iv| iv*jv }.min_by{|v| (v-Target).abs }, answer].min_by{|v| (v-Target).abs }
	a.pop
end
p answer

 @2011-04-14

まったく恥ずかしい。答えが合わないとなって当然問題を読み直してはいたんだけど、日を置いて改めて読んでみたら問題が何を求めてるのかが見えてきた。"nearest solution" ではなく "area" だったとさ。

Target = 2_000_000
Size = Math.sqrt(Target*2).floor+1
a = (1..Size).to_a
answer = [0,0]
until a.empty?
	j = a.last
	answer = ([answer] + a.map{|i| [i,j] }).min_by{|i,j| (i*(i+1)/2*j*(j+1)/2 - Target).abs }
	a.pop
end
puts "#{answer[0]} * #{answer[1]} = #{answer[0]*answer[1]}"

最終更新: 2014-04-25T14:53+0900

♪ [ProjectEuler] Problem 81, 82, 83

 Problem 81

迷路より簡単。右下から左上に向かって、右の要素と下の要素を参照しながら順番に処理するだけ。

matrix = DATA.lines.map{|ln| ln.chomp.split(",").map(&:to_i) }
raise "正方行列でない！" if matrix.size != matrix[0].size
(matrix.size-1).downto(0){|i|
	(matrix[i].size-1).downto(0){|j|
		incr = nil
		incr = matrix[i][j+1] if j+1 < matrix[i].size
		incr = matrix[i+1][j] if i+1 < matrix.size && (!incr || matrix[i+1][j] < incr)
		matrix[i][j] += incr if incr
	}
}
p matrix[0][0]
__END__
content of matrix.txt here.

 Problem 82

まだまだ簡単。最下段から、行を右へ左へ処理しながら上へ向かうだけ。こういう、問題・入力に依存して可変長のメモリを確保したりしない、そのうえ問題を単純に走査するだけの解法は安心できる。

Matrix = DATA.lines.map{|ln| ln.chomp.split(",").map(&:to_i) }.transpose # transpose:問いの右から左が、下から上への処理になる。
Order = Matrix.size
raise "正方行列でない！" if Matrix.size != Matrix[0].size

row = Matrix[0].dup # 1-line memo. row is now at the first(top) line of Matrix.
1.upto(Order-1){|i|
	# move from up ↓↓↓↓↓↓↓↓↓↓
	0.upto(Order-1){|j|
		row[j] += Matrix[i][j]
	}

	next if i == Order-1 # 最後の行は横移動不要(※禁止ではない)。最小値だけを選び取って答えにするから。

	# move right →→→→→→→→→→
	0.upto(Order-2){|j|
		src, dst, move_cost = row[j], row[j+1], Matrix[i][j+1]
		row[j+1] = src + move_cost if src + move_cost < dst
	}

	# move left ←←←←←←←←←←
	(Order-1).downto(1){|j|
		src, dst, move_cost = row[j], row[j-1], Matrix[i][j-1]
		row[j-1] = src + move_cost if src + move_cost < dst
	}
}
p row.min
__END__
content of matrix.txt here.

Array#transposeを使う機会があるなんて思わなかった！好きなメソッドは transpose(今日だけ)。ま、使わなくてもいいんだけど線形にアクセスするために。ま、メモリ構造からは遠く離れた Rubyなんだけど。

 @2013-05-11 アップデート

N×N確保していた作業メモを 1行分だけで済ませるようにスクリプトを修正。

コメントに「transpose:問いの右から左が、下から上への処理になる。」ってあるけど、今問題文を見ると左から右になってる。まあ、どっちからどっちでも変わらないからね。問題文が左から右になったからってわけではないけど、アップデート後は上から下の処理に変えてる。下から上だと、どうしてもその必然性を探してしまうから。

 Problem 83

シリーズの締め。迷路のときとは違って 80×80ともなると手当たりしだいに探索の手を伸ばしていくと 10分以上の時間がかかる。優先度を付けると insertのコストが加わったにもかかわらず、笑っちゃうぐらい一瞬で終わった。

C++だったら queueの実装として std::multimapを使うところだけど配列をヒープ構造にするのもありだ。

Matrix = DATA.lines.map{|ln| ln.chomp.split(",").map(&:to_i).freeze }.freeze
raise "正方行列でない！" if Matrix.size != Matrix[0].size
matrix = Matrix.map{|ln| Array.new(ln.size) }
size = matrix.size
moved = lambda{|i,j, l,m|
	return false if not (0...size).include?(l) or not (0...size).include?(m)
	src, dst, move_cost = matrix[i][j], matrix[l][m], Matrix[l][m]
	return false if dst && dst < src + move_cost

	matrix[l][m] = src + move_cost
	return true
}
matrix[0][0] = Matrix[0][0]
queue = [[0,0]]
insert = lambda{|l,m|
	val = matrix[l][m]
	queue.insert(queue.index{|i,j| val <= matrix[i][j] }||queue.size, [l,m])
}
until queue.empty?
	i,j = *(queue.shift)
	break if matrix.last.last and matrix.last.last <= matrix[i][j]
	[[i-1,j],[i+1,j],[i, j-1],[i,j+1]].each{|l,m|
		if moved[i,j, l,m]
			insert[l,m]
		end
	}
end
p matrix.last.last
__END__
content of matrix.txt here.

<queue>ヘッダには priority_queueクラスがあるし、<algorithm>には make_heap, pop_heap, push_heap といった、配列(RandomAccessIteratorをそなえたコンテナ)にかぶせて使うための関数があった。そりゃあるわなあ。ソートキーが要素のみから算出できない今回の場合に priority_queueを使う(外部キー)か、multimapを使う(内部キー)かはやっぱり決めかねるけど。

最終更新: 2011-03-21T02:43+0900

♪ [ProjectEuler] Problem 76, 77, 78

 Problem 76

Problem 31と同じ問題。その解答(20110125p01.03)。ただし、Problem 31には通用した俺の解法では全然終わらない。

Target = 100
a = [1] + [0]*Target
(Target-1).downto(1){|pick|
	0.upto(Target-pick){|i|
		a[i+pick] += a[i]
	}
}
p a[Target]

 Problem 77

素数ごとに一から再試行してるけど計算量はたかがしれてた。

require 'mathn'
prime_gen = Prime.new
primes = []
prime_gen.each{|prime|
	primes.push prime

	a = [1] + [0]*prime
	primes.each{|pr|
		0.upto(prime-pr){|i|
			a[i+pr] += a[i]
		}
	}

	answer = a.index{|x| 5000 < x }
	if answer
		p answer
		exit
	end
}

 Problem 78

まったくひどい解答。76から続くシリーズの締めらしく、何も考えないと計算量が膨大になる。手続き的な解法から一歩進む必要がある。それか一分ルールを無視して何時間もかけて良しとするか。

Target = 100000
a = [1] + [0]*Target
(Target-1).downto(1){|pick|
	0.upto(Target-pick){|i|
		a[i+pick] += a[i]
	}
}
p a.index{|x| x%1_000_000 == 0}

最終更新: 2012-02-29T17:34+0900

♪ [ProjectEuler] Problem 72

 Problem 72

前のバージョンはここ(20110312p01.02)。step2を最適化*すると倍くらい速くなって 1分半(ウチのPC基準で。C++だとコンマ1秒)。それに伴い素因数の組み合わせを求める必要がなくなったので、100万要素の配列の配列が 100万要素の Fixnum配列になってメモリ使用量が再び数MBレベルになった。

LIMIT = 1_000_000
pfs = Array.new(LIMIT+1, 1)
count = LIMIT*(LIMIT+1)/2 - 1 # 1) 2からLIMIT以下の分母 d につき d 通りの分子を予め計上する。
2.upto(LIMIT){|d| # 0) 2からLIMIT以下の分母 d に対して、
	print d,"\r"
	d.step(LIMIT, d){|_| pfs[_] *= -d } if pfs[d] == 1
	# 2) 分子が d で分母が d の倍数になるものを加減する。
	count += pfs[d]/pfs[d].abs * (LIMIT/d)*(LIMIT/d+1)/2 if pfs[d].abs == d
}
p count

一週間後にはこのコードが理解できなくなってること請けあい。

ググった>「Dreamshire | Project Euler Problem 72 Solution」。φ関数の値を合計するとかで、Rubyでも10秒未満。Problem 69に出てきた関数だけど、その問題はインチキしたから理解してないんよね。

LIMIT = 1000000
phi = (0..LIMIT).to_a
2.upto(LIMIT){|n|
	n.step(LIMIT, n){|m|
		phi[m] *= (n-1.0)/n
	} if phi[n] == n
}
p phi.inject(&:+).floor-1

繰り返しの構造は似てるのにこの実行時間の差はなんだ？ と思ったら print d,"\r" の有無だけだった。俺のも同等に速い。